

- Introduction
- Create a graph
- Run the algorithm
- Description of the algorithm
- Exercise 1
- Exercise 2
- More
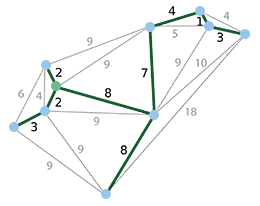
Minimum spanning tree (MST) shown in green!
The Minimum Spanning Tree Algorithm
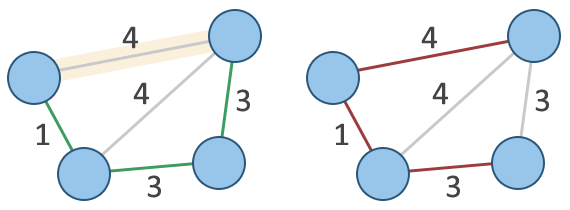
A telecommunication company wants to connect all the blocks in a new neighborhood. However, the easiest possibility to install new cables is to bury them alongside existing roads. So the company decides to use hubs which are placed at road junctions. How can the installation cost be minimized if the price for connecting two hubs corresponds to the length of the cable attaching them?
Considering the roads as a graph, the above example is an instance of the Minimum Spanning Tree problem. Prim's and Kruskal's algorithms are two notable algorithms which can be used to find the minimum subset of edges in a weighted undirected graph connecting all nodes.
This tutorial presents Prim's algorithm which calculates the minimum spanning tree (MST) of a connected weighted graphs. For a comparison you can also find an introduction to Kruskal's algorithm.
What do you want to do first?
Which graph do you want to execute the algorithm on?
Start with an example graph:
Modify it to your desire:
- To create a node, make a double-click in the drawing area.
- To create an edge, first click on the output node and then click on the destination node.
- The edge weight can be changed by double clicking on the edge.
- Right-clicking deletes edges and nodes.
Download the modified graph:
DownloadUpload an existing graph:
What next?
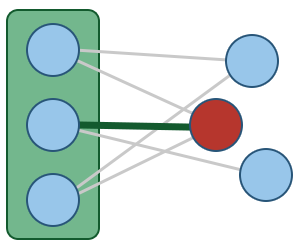
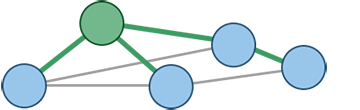
Legend
 |
Root Node, an arbitrary node which is used as the root of MST. |
 |
Node that is currently being processed |
 |
Node that is in the queue |
 |
Edge used for building Minimum Spanning Tree. |
Legend
Algorithm status
BEGIN
T ← ∅
FOR i ← 1, ..., n DO
d(v[i]) ← ∞, parent(v[i]) ← NULL
d(v[1]) ← 0, parent(v[1]) ← v[1]
WHILE queue ≠ ∅ DO
u ← queue.extractMin()
IF parent(u) ≠ u
T.add({parent(u), u})
FOR ALL {u, w} ∈ E do
IF w ∈ queue AND l(u, w) < d(w) THEN
d(w) ← l(u, w), parent(w) ← u
ELSE IF parent(w) = NULL THEN
d(w) ← l(u, w), parent(w) ← u
queue.insert(w)
END
Queue:
Task is terminated if the tab is changed.
You can open another browser window for reading the description in parallel.
Legend
 |
Root Node, an arbitrary node which is used as the root of MST. |
 |
Node removed from the queue |
Legend
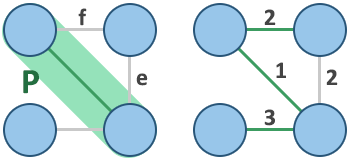
In which order are the nodes removed from the queue?
In which order are the nodes removed from the queue?
Your task is to click on the nodes of the graph in the order they are removed from the queue.
This corresponds to the order which the nodes were marked red during the execution of the algorithm.
Task is terminated if the tab is changed.
You can open another browser window for reading the description in parallel.
Legend
 |
Root Node, an arbitrary node which is used as the root of MST. |
 |
Node that is currently being processed |
 |
Node that is in the queue |
 |
Edge used for building Minimum Spanning Tree. |
Legend
Test your knowledge: How does the algorithm decide?
BEGIN
T ← ∅
FOR i ← 1, ..., n DO
d(v[i]) ← ∞, parent(v[i]) ← NULL
d(v[1]) ← 0, parent(v[1]) ← v[1]
WHILE queue ≠ ∅ DO
u ← queue.extractMin()
IF parent(u) ≠ u
T.add({parent(u), u})
FOR ALL {u, w} ∈ E do
IF w ∈ queue AND l(u, w) < d(w) THEN
d(w) ← l(u, w), parent(w) ← u
ELSE IF parent(w) = NULL THEN
d(w) ← l(u, w), parent(w) ← u
queue.insert(w)
END
Task is terminated if the tab is changed.
You can open another browser window for reading the description in parallel.