

- Introduction
- Create a graph
- Run the algorithm
- Description of the algorithm
- Exercise 1
- Exercise 2
- Exercise 3
- More
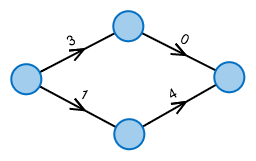
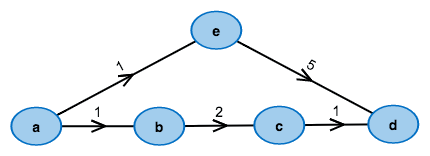
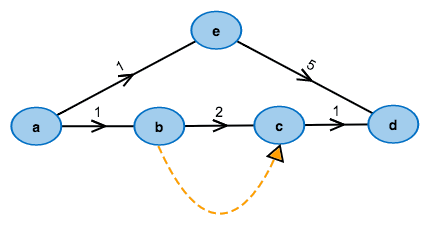
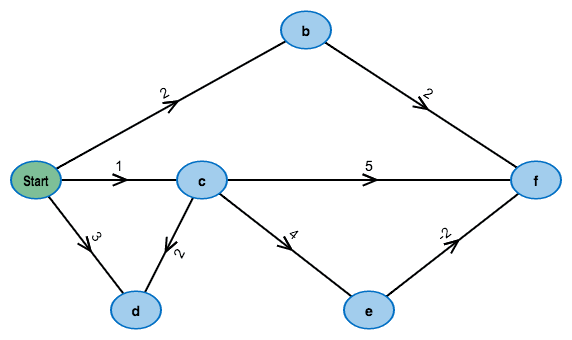
What's the cheapest way from left to right?
The classic among shortest path algorithms
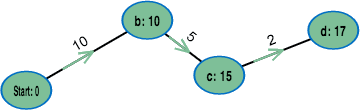
You want to know, how to get from Munich to Cologne as fast as possible? Is the fastest route via Stuttgart or via Frankfurt? Dijkstra's Algorithm can help you! With this algorithm, you can find the shortest path in a graph. The vertices of the graph can, for instance, be the cities and the edges can carry the distances between them.
Dijkstra's Algorithm can also compute the shortest distances between one city and all other cities. And the edges can describe costs, distances, or some other measure that is helpful for the user.
An important restriction of Dijkstra's Algorithm is, that all edge costs (which is how we call the edge labels) must not be negative.
This applet presents Dijkstra's Algorithm, which calculates shortest paths in graphs with positive edge costs.
What do you want to do first?
Which graph do you want to execute the algorithm on?
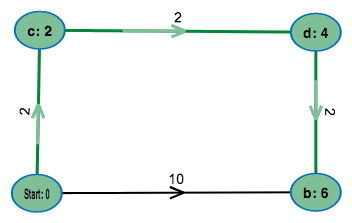
Start with an example graph:
Modify it to your desire:
- To create a node, make a double-click in the drawing area.
- To create an edge, first click on the output node and then click on the destination node.
- The edge weight is changed with a double-click on the edge.
- Right-clicking deletes edges and nodes.
Download the modified graph:
DownloadUpload an existing graph:
What next?
Legende
 |
Starting node from where distances and shortest paths are computed. |
 |
Node being processed. |
 |
Node in the priority queue. |
 |
"Predecessor edge" that is used by the shortest path to the node. |
Legend
Algorithm status
BEGIN
d(v[1]) ← 0
FOR i = 2,..,n DO
d(v[i]) ← ∞, parent(v[i]) ← NULL
WHILE queue ≠ ∅ DO
u = queue.extractMin()
FOR ALL (u,w) ∈ E DO
dist ← d(u) + l(u,w)
IF w ∈ queue AND d(w) > dist DO
d(w) = dist, parent(w) = (u,w)
ELSE IF parent(w) == NULL THEN
d(w) = dist, parent(w) = (u,w)
queue.insert(w,dist)
END
Priority Queue:
Task is terminated if the tab is changed.
You can open another browser window for reading the description in parallel.
Legend
 |
Starting node from where distances and shortest paths are computed. |
 |
Node that has been chosen correctly. |
Legend
How are the nodes in the priority queue ordered?
Changing the tab aborts the exercise!
You can open another browser window, to read the description in parallel.
Legend
 |
Starting node from where distances and shortest paths are computed. |
 |
Edge with currect edge costs. |
 |
Edge with wrong edge costs. |
Legend
What are the edge costs?
Node distances:
| Start | b | c | d | e | f | g | h | i | |
|---|---|---|---|---|---|---|---|---|---|
| Initiali- sation |
0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| Step 1 | 3 | 2 | 4 | 34 | |||||
| Step 2 | 14 | ||||||||
| Step 3 | 12 | 13 | |||||||
| Step 4 | 6 | 8 | |||||||
| Step 5 | 12 | 7 | |||||||
| Step 6 | 8 | 37 | |||||||
| Step 7 | 36 | ||||||||
| Step 8 | 35 | ||||||||
| Step 9 | 35 |
What are the edge costs?
This table shows all distances from the node to the starting node during every round of the algorithm. Some cells in the table are empty.
Can you find out the costs for these edges? Just doubleclick on an edge and set its cost.
The task is terminated if the tab is changed
You can open another browser window for reading the description in parallel.
Legend
 |
Starting node from where distances and shortest paths are computed. |
 |
Node being processed |
 |
Node in the priority queue |
 |
"Predecessor edge" that is used by the shortest path to the node. |
Legende
Test your knowledge: How does the algorithm decide?
BEGIN
d(v[1]) ← 0
FOR i = 2,..,n DO
d(v[i]) ← ∞, parent(v[i]) ← NULL
WHILE queue ≠ ∅ DO
u = queue.extractMin()
FOR ALL (u,w) ∈ E DO
dist ← d(u) + l(u,w)
IF w ∈ queue AND d(w) > dist DO
d(w) = dist, parent(w) = (u,w)
ELSE IF parent(w) == NULL THEN
d(w) = dist, parent(w) = (u,w)
queue.insert(w,dist)
END
Task is terminated if the tab is changed.
You can open another browser window for reading the description in parallel.