

- Einführung
- Graph erstellen
- Algorithmus ausführen
- Beschreibung des Algorithmus
- Forschungsaufgabe 1
- Forschungsaufgabe 2
- Weiteres
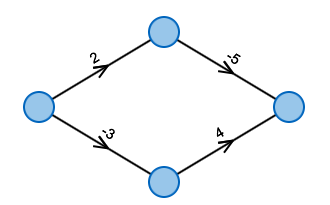
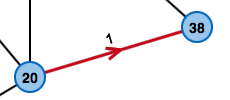
Wie komme ich am günstigsten von links nach rechts?
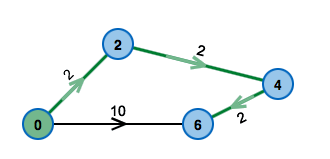
Kürzeste Wege und günstigste Wege
In vielen Anwendungen kann es nützlich sein, den kürzesten Weg von a nach b zu berechnen. Dabei muss die Länge eines Weges nicht unbedingt die Länge in Metern sein: Genauso gut kann man die Kosten eines Weges betrachten – man sucht also den günstigsten Weg.
Hier wird der Bellman-Ford-Algorithmus vorgestellt, der günstigste Wege auch bei negativen Kosten berechnet.
Was möchtest du zuerst tun?
Auf welchem Graph soll der Algorithmus ausgeführt werden?
Nimm ein fertiges Beispiel!
Ändere den Graphen nach deinen Vorstellungen:
- Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
- Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
- Das Kantengewicht kann mit einem Doppelklick auf die Kante verändert werden.
- Ein Rechtsklick löscht Kanten und Knoten.
Lade den veränderten Graphen herunter:
DownloadLade einen existierenden Graphen hoch:
Was nun?
Legende
 |
Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden. |
 |
"Vorgängerkante", die der günstigste Weg zum Knoten benutzt. |
Legende
Status des Algorithmus
BEGIN
d(v[1]) ← 0
FOR j = 2,..,n DO
d(v[j]) ← ∞
FOR i = 1,..,(|V|-1) DO
FOR ALL (u,v) in E DO
d(v) ← min(d(v), d(u)+l(u,v))
FOR ALL (u,v) in E DO
IF d(v) > d(u) + l(u,v) DO
Meldung: "Negativer Kreis"
END
Status der Variablen:
| i | d(u) | d(v) | l(u,v) |
|---|---|---|---|
Beim Wechsel des Tabs wird der Algorithmus abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Legende
 |
Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden. |
 |
"Vorgängerkante", die der günstigste Weg zum Knoten benutzt. |
Legende
Prüfe dein Wissen: Wie würde der Algorithmus entscheiden?
BEGIN
d(v[1]) ← 0
FOR j = 2,..,n DO
d(v[j]) ← ∞
FOR i = 1,..,(|V|-1) DO
FOR ALL (u,v) in E DO
d(v) ← min(d(v), d(u)+l(u,v))
FOR ALL (u,v) in E DO
IF d(v) > d(u) + l(u,v) DO
Meldung: "Negativer Kreis"
END
Beim Wechsel des Tabs wird die Aufgabe abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Legende
 |
Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden. |
 |
Kante, die bereits ausgewählt wurde. |
 |
Kante, die im letzten Schritt ausgewählt wurde. |
Legende
Wie ist die optimale Sortierung der Kanten?
Wie ist die optimale Sortierung der Kanten?
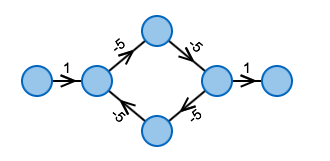
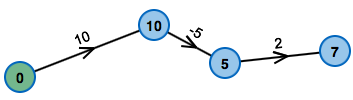
Der Bellman-Ford-Algorithmus kann schon nach einer einzigen Phase alle Entfernungen korrekt berechnet haben.
Dafür müssen die Kanten allerdings in der optimalen Reihenfolge betrachtet werden. Diese Reihenfolge ist aber nicht leicht zu finden – das dauert genauso lange wie der Bellman-Ford-Algorithmus selbst.
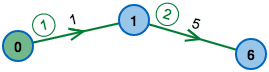
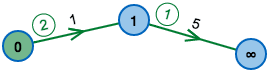
Im Beispiel sieht man: Links ist die Reihenfolge sinnvoll, der Algorithmus kann schon nach einer Runde alle Kosten korrekt berechnet haben. Rechts ist das nicht der Fall.
In dieser Aufgabe kannst du experimentieren, wie viele Phasen der Bellman-Ford-Algorithmus bei verschiedenen Sortierungen benötigt.
Beim Wechsel des Tabs wird die Aufgabe abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.