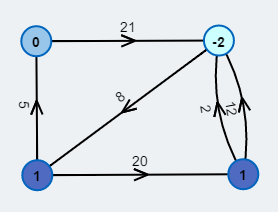
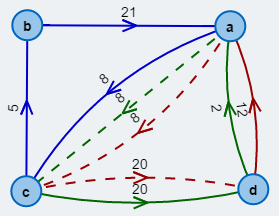
Ausgangsgraph.
Im Knoten ist die Differenz zwischen Ausgangsgrad und Eingangsgrad notiert.
Knoten mit der Differenz ungleich 0 sind unbalanciert.
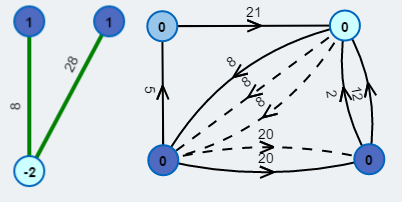
Links ist der bipartite Matching-Graph mit allen unbalancierten Knoten.
Hier wird bestimmt zwischen welchen Knoten neue Wege eingefügt werden. Rechts ist der Graph nach den Pfadeinfügungen.
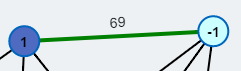
Matching-Kante.
Die Matching-Kanten geben an, zwischen welchen Knoten Pfade eingefügt werden müssen.
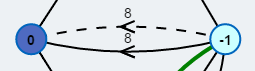
Neu eingefügte Kante.
Die gestrichelten Kanten repräsentieren das mehrfache Ablaufen einer Kante.
Eulertour.
Die verschiedenen Farben kennzeichnen die unterschiedliche Subtouren des Hierholzer-Algorithmus.
Briefträgerproblem
Ein typisches Beispiel für dieses Problem ist ein Postbote, der alle Straßen einer Stadt ablaufen muss und wieder zum Startpunkt zurückkehrt. Dabei will er eine möglichst kurze Distanz zurücklegen.
Das Problem lässt sich mit einem Graphen modellieren.
Ein Kantenzug ist eine Folge von Kanten im Graphen, sodass jede nächste Kante als Startknoten den Endknoten der vorherigen Kante besitzt.
Ein Kantenzug ist geschlossen, falls er wieder zum Startknoten der ersten Kante zurückkehrt.
Man nennt einen geschlossenen Kantenzug Eulerkreis (Eulertour), falls er alle Kanten eines Graphen genau einmal enthält.
Das Briefträgerproblem besteht darin, einen geschlossenen Kantenzug (Rundgang) im Graphen zu finden, sodass alle Kanten mindestens einmal
benutzt werden und die Summe der Kantengewichte des Kantenzugs (Kosten des Rundgangs) minimal ist.
Idee des Algorithmus
Da Knoten ohne Eingangs- und Ausgangskanten keinen Einfluss auf die Lösung des Problems haben, können wir annehmen, dass solche isolierten Knoten nicht existieren.
Das Problem ist genau dann lösbar, wenn der Graph stark zusammenhängend ist (jeder Knoten ist von jedem Knoten aus erreichbar) und keine negativen Kreise (geschlossener Kantenzug im Graphen, sodass die Summe der Gewichte der Kanten negativ ist) existieren.
Wenn der Graph nicht stark zusammenhängend ist, gibt es keinen Rundgang und wenn ein negativer Kreis existiert, werden die Kosten unendlich klein.
Das Problem lässt sich auf das Bestimmen einer Eulertour im Graphen zurückführen. Falls es eine Eulertour im Graphen gibt,
ist diese Tour das optimale Ergebnis, da jede Kante genau einmal besucht wird. Im anderen Fall müssen einige Kanten mehrmals besucht werden. Diese Situation lässt sich modellieren, indem
wir zusätzliche Kanten in den Graphen einfügen, die mehrfach benutzten Kanten repräsentieren (mit dem gleichen Kantengewicht wie die originale Kante). Dann besitzt der Rundgang die gleichen Kosten, wie
die Eulertour im neuen Graphen. Das Problem besteht jetzt darin, die mehrfach benutzten Kanten des minimalen Rundgangs zu bestimmen.
Die Anzahl der Eingangskanten eines Knotens nennt man den Eingangsgrad und die Anzahl der Ausgangskanten den Ausgangsgrad des Knotens.
Ein Theorem der Graphentheorie besagt, dass es genau dann eine Eulertour im Graphen gibt, wenn bei allen Knoten im Graphen der Eingangsgrad mit dem Ausgangsgrad übereinstimmt.
Also reicht es aus, wenn wir zusätzliche Pfade in den Graphen einfügen, sodass nach dem Einfügen bei allen Knoten im Graphen der Eingangsgrad mit dem Ausgangsgrad übereinstimmt.
Die Summe der Kantengewichte der Pfade sollte minimal sein.
Welche Pfade genau eingefügt werden, wird im Matching-Schritt des Algorithmus festgestellt.
Nachdem sichergestellt wurde, dass der Graph eine Eulertour besitzt, muss diese nur gefunden werden. Dies erfolgt mit einem geeigneten Algorithmus, wie zum Beispiel dem Hierholzer-Algorithmus.
Die Kosten des optimalen Rundgangs werden durch die Summe aller Kantengewichte der Eulertour bestimmt.
Kürzeste Wege
Von den Knoten mit zu wenigen Ausgangskanten müssen Wege zu den Knoten mit zu wenigen Eingangskanten hinzugefügt werden. Da die Kosten minimal sein sollten, kommen nur die kürzesten Wege in Frage.
Um die kürzesten Wege zu bestimmen, wird der Algorithmus von Floyd-Warshall benutzt.
Der Floyd-Warshall-Algorithmus eignet sich sehr gut an dieser Stelle, da er die kürzesten Wege zwischen allen Knotenpaaren berechnet.
Die Kosten der kürzesten Wege werden im Matching-Schritt benutzt, um die optimale Menge von Wegen zu finden.
Matching
Durch Einfügen zusätzlicher Pfade wollen wir erreichen, dass bei allen Knoten im Graphen der Eingangsgrad mit dem Ausgangsgrad übereinstimmt. Dann existiert eine Eulertour im Graphen.
Wir bezeichnen mit \(\delta_v\) die Differenz zwischen Ausgangs- und Eingangsgrad eines Knotens v. Alle Knoten v mit \(\delta_v \neq 0 \) werden als unbalanciert bezeichnet.
Um zu bestimmen welche Pfade wir einfügen, muss eine Zuordnung von Knoten
mit negativen \(\delta_v\) zu den Knoten mit positiven \(\delta_v\) erfolgen. Dabei bestimmt \(\delta_v\) die Anzahl der neuen Pfade, die in dem Knoten v anfangen bzw. enden müssen.
Ein Pfad vergrößert die Differenz zwischen Ausgangs- und Eingangsgrad des Startknotens um eins und verringert die des Zielknotens um eins.
Das Gewicht der zusätzlichen Pfade sollte minimal sein. Um dieses Ziel zu erreichen erstellt man einen neuen bipartiten Graphen, der alle unbalancierten Knoten enthält.
Die unbalancierten Knoten werden in zwei Knotenmengen unterteilt (negatives und positives \(\delta_v\)).
\(\delta_v\) bestimmt wie viele Exemplare des Knotens v im bipartiten Graph vorkommen. Zum Beispiel existieren von einem Knoten v mit \(\delta_v=3\) genau 3 Kopien im Matching-Graphen.
Bei der Visualisierung des Algorithmus wurde darauf verzichtet mehrere Exemplare eines Knoten darzustellen, damit die Übersicht nicht verloren geht.
Stattdessen wird für einen unbalancierten Knoten genau ein Knoten im Matching-Graphen dargestellt.
Die Knoten in der Visualisierung des Matching-Graphs liegen dann möglicherweise auf mehr als einer Matching-Kante (dies wird durch \(\delta_v\) bestimmt).
Das Gewicht einer Kante im Matching-Graphen stellt die Länge des kürzesten Pfades von dem Knoten mit negativer Differenz zwischen dem Ausgangs- und dem Eingangsgrad zu dem Knoten mit positiver Differenz dar.
Die Summe der Eingangsgrade und der Ausgangsgrade ist in einem Graphen ausgeglichen. Dann ist die Summe der positiven \(\delta_v\) und der negativen \(\delta_v\) ebenfalls ausgeglichen.
Damit erhalten wir einen vollständigen bipartiten Graphen. Wir wenden einen Algorithmus zur Lösung von gewichteten Matchings auf diesen Graphen an, wie zum Beispiel die
Ungarische Methode. Damit erhalten wir die optimale Zuordnung und können die neuen Pfade einfügen.
Die Kanten der Pfade repräsentieren die Kanten des optimalen Rundgangs, die mehrfach benutzt werden.
Eulertour
Nach dem Einfügen von zusätzlichen Pfaden, besitzen alle Knoten im Graphen die gleiche Anzahl von Eingangs- und Ausgangskanten.
Dann existiert ein Eulerkreis im Graphen. Um diesen zu finden, wird der Algorithmus von Hierholzer verwendet.
Die Kosten des optimalen Rundgangs werden durch die Summe aller Kantengewichte der Eulertour bestimmt.
Was nun?
Einen Graph erstellen und den Algorithmus durchspielen
Sein Wissen an den Forschungsaufgaben testen