Der Blossom Algorithmus von Edmonds
Der Blossom Algorithmus von Edmonds

Größte Matchings in allgemeinen Graphen
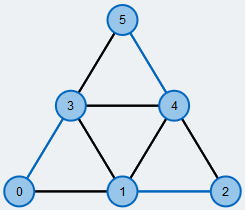
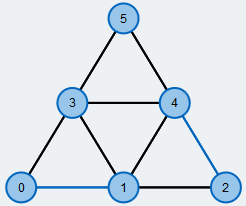
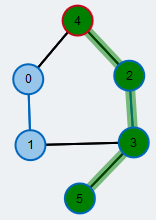
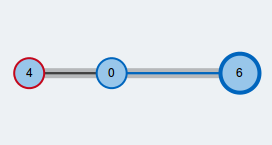
Größtes Matching in einem Graphen.
Kanten des Matchings sind blau markiert.
Ein oft genutztes und intensiv erforschtes Problem der Graphentheorie ist die Berechnung eines größten Matchings in einem Graph \( G=(V,E)\). Ein Matching M ist dabei eine Teilmenge der Kanten, so dass jeder Knoten von maximal einer Kante des Matchings getroffen wird. M ist ein größtes Matching, falls kein anderes Matching in G mehr Kanten als M hat.
Diese Seite stellt den Blossom Algorithmus von Edmonds vor, welcher ein größtes Matching in einem ungerichteten Graphen berechnet. Im Gegensatz zu anderen Matching-Algorithmen muss der Graph hierbei nicht bipartit sein. Der Algorithmus wurde 1965 von Jack Edmonds vorgestellt und wurde seither noch auf verschiedene Arten weiterentwickelt und verbessert. Viele moderne Verfahren zur Berechnung von größten Matchings in allgemeinen Graphen basieren auch heute noch auf der Grundidee des Blossom Algorithmus.
Der Blossom Algorithmus von Edmonds nutzt und erweitert die grundsätzliche Idee des Hopcroft-Karp Algorithmus, welcher größte Matchings auf bipartiten Graphen berechnet. Falls du den Algorithmus noch nicht kennst, empfehlen wir dir ihn vorher kurz anzusehen: Hopcroft-Karp Algorithmus
Weiterhin nehmen wir an, dass grundlegende Methoden der Graphsuche wie die Breitensuche bekannt sind.
Dieses Applet gibt eine Visualisierung und detaillierte Erklärung des Blossom Algorithmus wieder. Du kannst einen beliebigen Graphen erstellen, auf diesem Graphen ein größtes Matching berechnen und mehr über die theoretischen Hintergründe des Algorithmus lernen.
Was möchtest du zuerst tun?
Auf welchem Graph soll der Algorithmus ausgeführt werden?
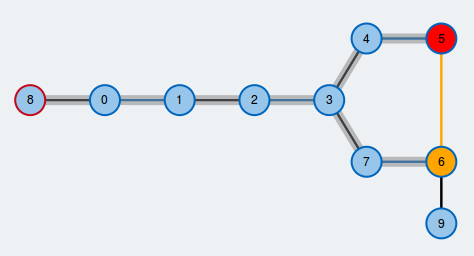
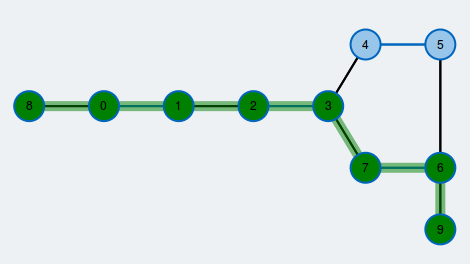
Nimm ein fertiges Beispiel!
Ändere den Graphen nach deinen Vorstellungen:
- Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
- Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
- Ein Rechtsklick löscht Kanten und Knoten.
Lade den veränderten Graphen herunter:
DownloadLade einen existierenden Graphen hoch:
Was nun?
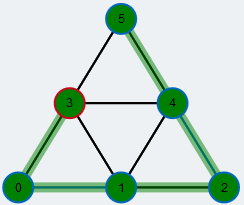
Legende
 |
gelb: freier Knoten |
 |
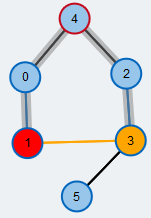
rot umrandet: Wurzel der BFS |
 |
rot: aktuell aktiver Knoten der BFS |
 |
orange: aktuell betrachteter Nachbar in BFS |
 |
grün: Knoten auf augmentierendem Pfad |
 |
großer Knoten: kontrahierter Knoten |
 |
orange: aktuell betrachtete Kante der BFS |
 |
blau: Kante in Matching |
 |
grau hinterlegt: Kante in BFS Baum |
 |
grün hinterlegt: Kante in augmentierendem Pfad |
Legend
Status des Algorithmus
Blossom Algorithmus von Edmonds
Der Algorithmus kann nun beginnen. Klicke auf "Nächster Schritt", um den nächsten Schritt des Algorithmus auszuführen. Klicke auf "Zurück", um den letzten Schritt rückgängig zu machen, und auf "Vorspulen", um den Algorithmus schnell auszuführen.
Breitensuche fertig
Die BFS Liste ist leer. Die modifizierte Breitensuche hat keinen augmentierenden Pfad gefunden.
Verbessertes Matching
Der augmentierende Pfad wird invertiert, um das Matching zu vergrößern. Dies bedeutet, dass alle nicht im Matching enthaltenen Kanten des augmentierenden Pfades ins Matching aufgenommen werden, und die vorher im Matching enthaltenen Kanten des Pfades aus dem Matching entfernt werden. Dadurch erhöhrt sich die Anzahl der Kanten im Matching um 1. Das neue Matching ist blau markiert.
Freie Knoten vorhanden
Es gibt noch vom Matching nicht überdeckte Knoten (gelb). Wir nennen sie freie Knoten. Wir versuchen nun, einen augmentierenden Pfad zu finden und damit das Matching zu vergrößern. Ein augmentierender Pfad beginnt und endet an einem freien Knoten und nutzt dazwischen abwechselnd im Matching und nicht im Matching enthaltene Kanten.
Beginne Breitensuche
Wir wählen einen der freien Knoten als Wurzel der modifizierten Breitensuche (BFS). Er wird für die Dauer der Breitensuche rot umrandet. Ausgehend von der gewählten Wurzel konstruieren wir einen Baum bestehend aus alternierenden Pfaden (den BFS Baum), bis wir einen anderen freien Knoten erreichen.
Nehme nächsten Knoten der BFS Liste
Ausgehend vom aktuellen Knoten können wir keine weiteren Nachbarn überprüfen. Deshalb führen wir die Breitensuche beim nächsten Knoten in der Liste fort.
Kontrahiere Blossom
Der gefundene Kreis ungerader Länge wird zu einem Pseudoknoten kontrahiert. Pseudoknoten werden im Graphen größer dargestellt. Wir fügen den neuen Pseudoknoten zusätzlich in die BFS Liste ein.
Führe Breitensuche mit nächstem Knoten fort
Nehme den nächsten Knoten aus der BFS Liste. Wir nennen diesen Knoten unseren aktiven Knoten und markieren ihn rot. Ausgehend von diesem Knoten werden wir die Nachbarn betrachten und einen freien Knoten suchen.
Erweitere BFS Baum
Wir fügen den Nachbarn und seinen Matchingpartner in den BFS Baum ein. Der Matchingpartner wird zudem in die BFS Liste eingefügt und wird eventuell später wieder betrachtet. Die Kanten im BFS Baum werden grau hervorgehoben.
Ignoriere Kreis gerader Länge
Wir können Kreise gerader Länge ignorieren. In dem Fall geschieht deshalb nichts Weiteres.
Betrachte nächsten Nachbarn
Wir überprüfen den nächsten Nachbarn (orange) und sehen, dass er bereits vom Matching überdeckt ist.
Betrachte nächsten Nachbarn
Wir überprüfen den nächsten Nachbarn (orange) und sehen, dass er ein freier Knoten ist (gelb). Wir haben deshalb einen augmentierenden Pfad zwischen der Wurzel der Suche und diesem Nachbarn gefunden.
Betrachte nächsten Nachbarn
Wir überprüfen den nächsten Nachbarn (orange) und sehen, dass er bereits in der BFS Liste enthalten ist. Wir wissen deshalb, dass ein Kreis existiert, welcher zudem eine ungerade Kantenzahl hat. Wir nennen solch einen Kreis eine Blüte (Blossom).
Betrachte nächsten Nachbarn
Wir überprüfen den nächsten Nachbarn (orange) und sehen, dass er bereits in der BFS Liste enthalten ist. Wir wissen deshalb, dass ein Kreis existiert, welcher zudem eine gerade Kantenzahl hat.
Rekonstruiere den augmentierenden Pfad
Der augmentierende Pfad ist grün markiert. Bevor wir das Matching vergrößern, müssen wir die kontrahierten Pseudoknoten wieder expandieren.
Expandiere Pseudoknoten
Einer der Pseudoknoten wurde expandiert und der augmentierende Pfad entsprechend angepasst. Es gibt noch weitrere Pseudoknoten, welche expandiert werden müssen.
Rekonstruiere den augmentierenden Pfad
Der augmentierende Pfad von der Wurzel der Breitensuche zum freien Knoten wurde vollständig rekonstruiert und ist grün markiert.
Rekonstruktion des augmentierenden Pfades fertig
Nach der Expansion aller Pseudoknoten ist der augmentierende Pfad vollständig rekonstruiert und grün markiert.
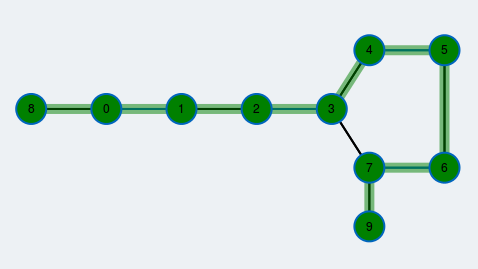
Algorithmus abgeschlossen
Im Graph sind keine freien Knoten mehr vorhanden, wir haben also ein größtes Matching gefunden. Es ist blau markiert.
BEGIN
WHILE F != ∅ DO (*freie Knoten F*)
wähle r ∈ F
queue.push(r) (*BFS Liste*)
T ← ∅ (*BFS Baum T*)
T.add(r)
WHILE queue != ∅
v ← queue.pop()
FOR ALL Nachbarn w von v DO
IF w ∉ T AND w in Matching THEN
T.add(w)
T.add(Matchingpartner(w))
queue.push(Matchingpartner(w))
ELSE IF w ∈ T AND gerader Kreis THEN
CONTINUE
ELSE IF w ∈ T AND ungerader Kreis THEN
kontrahiere Kreis
ELSE IF w ∈ F THEN
expandiere alle kontrahierten Knoten
rekonstruiere augm. Pfad
invertiere augm. Pfad
END
Beim Wechsel des Tabs wird der Algorithmus abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.